Лефшец-наперстки та квантові фази в нульвимірних бозонових моделях
Анотація
У цій роботі, аналізуючи структуру Лефшеца-наперстка, ми досліджуємо квантові фази (або квантові критичні точки) в теоріях нульового виміру скалярного поля зі складними діями. Використовуючи перші принципи, ми отримуємо рівняння накидків цих моделей для різних значень параметрів зв'язку. При розкладанні наперстків складних інтегралів шляху визначення важливих складових виступає визначення так званих чисел перетину. У цій роботі ми отримуємо аналітичні вирази для комбінованого числа перетинів наперстків та антинаперстків цих теорій нульових розмірів. Ми також отримуємо умовні вирази, що включають співвідношення між параметрами зв'язку моделі, які допоможуть нам передбачити квантові фазові переходи в цих системах. Ми бачимо, що основна структура наперстка зазнає кардинальних змін, коли система проходить такий фазовий перехід.
Вступ
Ми зустрічаємо інтеграли шляху зі складними діями у багатьох галузях фізики. Яскравими прикладами є інтеграл шляху Мінковського, теорія Янга – Міллса у тета-вакуумі, калібровані теорії Черна – Саймонса, хіральні калібровані теорії та КХД з хімічним потенціалом. Існують також квантові теорії зі складними діями, які інваріантні щодо \ (> \) симетрії [1,2,3]. В контексті теорії струн, матрична модель IKKT, нульвимірна суперсиметрична квантова теорія поля, яка служить перспективним кандидатом для непертурбативної формулювання теорії суперструн, має складний ферміонний оператор [4,5,6]. Дослідження непертурбативної структури таких теорій за допомогою традиційних методів інтегрального шляху Монте-Карло є ненадійним через наявність проблеми зі знаками. Було б дуже корисно мати формалізм, який пропонує перспективний інструмент для вирішення квантових теорій поля, що містять такі складні інтегральні вагові ваги.
Нещодавно розроблений метод боротьби з квантовими теоріями полів із складними діями використовує складний аналог теорії Морзе з диференціальної топології [7, 8]. Примітка 1. Там об’єкти першочергового інтересу, так звані наперстки Лефшеца, являють собою набір підколекторів, пов’язаних із функцією, яка задовольняє рівняння потоку Морзе для дійсної частини функції. Основною ідеєю використання цього формалізму є перетворення інтегралу шляху з точки зору скінченного набору не коливальних інтегралів. Нещодавні роботи над складними інтегралами траєкторій та з'єднаннями з наперстками Лефшеца, включаючи програми для квантового тунелювання та амплітуд розсіювання, можна побачити в посиланнях. [18,19,20,21,22,23,24,25,26,27,28,29]. У посиланнях [30,31,32,33,34,35] підхід Лефшеца-наперстка був використаний для вивчення теорій бозонових квантових полів, а також у посиланнях. Були вивчені [36,37,38,39,40,41,42,43] моделі, що включають ферміони. Актуальність наперстків Лефшеца в контексті напівкласичного розширення в асимптотично вільних квантових теоріях поля обговорюється в посиланнях. [44,45,46,47,48].
Стаття організована таким чином. У розд. 2 ми пропонуємо праймер на наперстках Лефшеца, вводячи рівняння градієнтного потоку даної дії. У розд. 3 ми представляємо модель, яка нас цікавить, нульвимірну бозонову модель зі складною дією, що містить квартові взаємодії та джерельний термін. Рівняння наперстків для цієї моделі виведені далі в розділі. 4. Ми обговорюємо аналітичні вирази для рівнянь наперстків та наперстків, а також так звані рішення для привидів, які не є ані наперстками, ані натяками. Ми також обговоримо поведінку функції розділення та спостережувані моделі як функції параметрів управління. У розд. 5 ми обговоримо межі фазових переходів для різних комбінацій значень параметрів зв'язку. Сюди входить цікавий випадок, коли складна дія виявляє \ (> \) симетрію. Кілька прикладів меж фазового переходу подано в Розділі. 6. Приклади показують, що структура наперсток зазнає різких змін, коли керуючі (нетеплові) параметри моделі проходять через квантово критичну точку. У розд. 7 ми подаємо короткий виклад основних результатів, і в Розділі. 8 ми даємо свої висновки та вказуємо можливі подальші напрямки.
Буквар на наперстках Лефшеца
Інтуїтивно ми можемо пов’язати наперстки Лефшеца з початковим циклом інтегрування квантової теорії поля наступним чином. Позначимо початковий цикл інтеграції як \ (> _ >> \). Ми 'ускладнюємо' цей множник до \ (> _ >> \), тобто беремо складний колектор \ (> _ >> \), що містить вихідний колектор \ (> _ >> \) як підмноговид, з вимога про те, що комплексно спряженим елементом \ (> _ >> \) є сам елемент. Можна полегшити поняття \ (> _ >> => ^ \) та \ (> _ >> => ^ \) для зручності розуміння.
Після комплексу, ми ідентифікуємо Функція Морзе [51]. Функція Морса в вільному сенсі визначає ці наперстки. Природною функцією, яку слід враховувати, є дія. (Фактична функція Морса, що розглядається, є дійсною частиною \ (- S \), оскільки, за визначенням, функції Морзе є реальними.) Враховуючи функцію Морса, ми ідентифікуємо її критичні точки - точки в \ (> _ >> \), де функція Морзе локально екстремізована. Наступним кроком, візуально, можна вважати постійно деформується \ (> _ >> \), деформація контролюється функцією Морса за допомогою рівнянь потоку Морзе
де \ (g ^> \) - метрика на \ (> _ >> \) та \ (z_\) - це набір локальних координат навколо критичних точок S. Це можна відразу перевірити, що уявна частина дії S є постійною вздовж розв'язку вищевказаних рівнянь.
Як остаточний результат цієї конструкції ми отримуємо пару підколекторів, які називаються наперстком і наперстком, пов’язаним з кожною критичною точкою. Наперсток - це «стабільне» рішення. Тобто дія рухається до нескінченності досить швидко вздовж наперстка, щоб інтеграл, що включає \ (\ exp (-S) \), збігався. Анти-наперсток - це «нестабільне» рішення. Прикладом, знайомим у фізиці, є метод найкрутішого спуску, і, отже, формалізм Лефшеца на наперстках можна розглядати як узагальнення методу найкрутішого спуску. Сувору обробку цієї конструкції можна знайти в посиланнях. [51,52,53].
Інтеграл, що включає дію на підрізноманітність \ (> _ >> \), тепер можна записати як лінійну комбінацію інтегралів над наперстками Лефшеца. У цій мові вираз для функції розділу, пов'язаної з системою з дією S дається як зважена сума внесків з критичних точок дії
де інтеграл позначає інтеграцію над наперстком Лефшеца \ (> _ i \), який пов'язаний з i-го критична точка \ (\ phi _i \) дії. Вага (також відомий як номер перетину) \ (n_i \) - це ціле число, яке визначає внесок певної критичної точки у функцію розділення. Припускаючи, що критичні точки не мають спільного градієнтного потоку, наведеного в рівнянні (2.1), \ (n_i \) визначається кількістю випадків, коли анти-наперсток перетинає початковий цикл інтеграції \ (> \) [54]. Це,
Перевага використання наперстків Лефшеца полягає в тому, що на цих наперстках, як обговорювалося вище, уявна частина дії залишається незмінною. Це, безумовно, бажана властивість, оскільки в (евклідовому) шляху інтегрального формалізму квантових теорій полів постійна уявна частина дії, \ (\ mathrm (S) \), в інтегралі, рів. (2.2), можна витягнути як фазовий коефіцієнт, а інтеграл, що залишився, стає інтегралом, що не коливається. Виноска 2
У вимірах нульового простору та часу формалізм значно спрощується. Для більшості ситуацій, розглянутих у цій роботі, початковий цикл інтеграції є дійсним, \ (> \). У цьому випадку ми в кінцевому підсумку маємо справу з кривими в площині дозволених ступенів свободи для полів (тобто \ (> \)), які задовольняють рівняння градієнтного потоку
де т є параметром, а накладене зображення являє собою складне спряження. Наперсток \ (_ i \), пов'язаний з критичною точкою \ (\ phi _i \) дії, визначається як рішення рівняння. (2.4), що задовольняє
і анти-наперсток \ (_ i \) задовольняє
За визначенням, наперстки завжди закінчуються всередині областей стабільності, виноска 3, тоді як наперстки закінчуються всередині областей нестабільності.
Квартична модель із вихідним терміном
Давайте розглянемо квантову теорію поля в нульово-просторово-часових вимірах із дією, поданою у наступному вигляді
Дія має квартовий термін взаємодії та джерельний термін - це найпростіша нетривіальна дія квантової теорії поля з джерельним терміном. Параметри \ (\ sigma \), \ (\ lambda \) та h є загалом складними. Для зручності ми також висловлюємо
Мотивація розгляду цієї конкретної дії подвійна. По-перше, вищевказана дія виступає як відмінна модель іграшки для розуміння систем із складними діями, на шляху інтегрального формалізму [34, 49, 55, 56], і як наперстки Лефшеца допомагають пом'якшити знак проблема, водночас не надто тривіальний і дозволяє продемонструвати багато багатої динаміки, яка супроводжує аналіз наперстків Лефшеца. Вищевказана дія із комплексом \ (\ sigma \) є релевантною для релятивістського бозе-газу з ненульовим хімічним потенціалом [57, 58]. Варіант цієї моделі із комплексами \ (\ sigma = h = 0 \) та \ (\ lambda \) вивчався в [3]. [55]. По-друге, для методу, використовуваного в наших розрахунках, квартічні взаємодії є найвищими, точно розв'язуваними членами завдяки теоремі Абеля – Руффіні в алгебрі [59], яка стверджує, що не існує виразів замкнутої форми для розв'язків загальних поліноміальних рівнянь ступеня п'ятого або вище. Крім того, включення вихідного терміна гарантує, що ми вичерпаємо всі фізично можливі ситуації для системи з квартовими взаємодіями.
Почнемо з визначення областей стабільності (іноді їх називають Стоксові клини [46, 77]) у цій моделі. Оскільки інтеграл у рівнянні (2.2) включає вираз \ (\ text (-S) \), інтеграл збігається в регіонах, де, як \ (\ phi \) наближається до нескінченності, \ (\ text (S [\ phi]) \ ge 0 \ ). Оскільки найвищий порядок у нашій дії - чотири, ми отримуємо чотири клини в комплексній площині, де інтеграл збіжний. Це схематично показано на рис. 1.
Схематичне зображення областей стійкості на нескінченності для дії, наведеної в рівнянні (3.1). Усередині затінених областей інтеграл в рівнянні (2.2) збіжна. Загалом положення і форма цих клинів контролюється параметрами \ (\ sigma, \ lambda \) та h в дії
Одним із способів знайти (анти) наперсток, пов'язаний з критичною точкою, є вирішення рівняння градієнтного потоку, рівняння (2.4), для (анти-) наперсток. Однак цей метод швидко стає дуже складним, навіть для простих форм дій, через зв'язок між реальною та уявною частинами диференціального рівняння. На щастя, існує ще один простіший метод. Ми можемо використати дуже важливу властивість (анти-) наперсток: уявна частина дії залишається незмінною вздовж цих (анти) наперстків. Тому, щоб вирішити наперстки, ми шукаємо рішення обмеження
з \ (\ phi _i \), що позначає критичну точку.
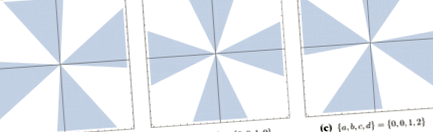
Рішення рівняння наперстка, наведені в рівнянні (3.3), що відповідає критичним точкам \ (\ phi _0 \) та \ (\ phi _ \ pm \), для параметрів \ (\< a = 1, b = 1, c = 1, d = 0, h = 0 \>\). На всіх трьох фігурах зелені суцільні криві представляють наперстки, червоні пунктирні криві - анти-наперстки, а сірі суцільні криві - привиди. Затінені області представляють регіони, де \ (\ text (S) \ ge 0 \)
Давайте обмежимо наші розрахунки випадками, коли h (параметр, що керує лінійним доданком у дії), малий порівняно з \ (\ sigma \) та \ (\ lambda \). Ми додатково обмежуємо h бути або справжнім, або суто уявним. Це дозволяє наблизити три критичні точки до виноски 4 дії як
Критична точка \ (\ phi _0 \) близька до початку координат (тобто \ (\ phi = 0 \)) для малих h тоді як позиція \ (\ phi _ \ pm \) залежить від вибору параметрів. Позначимо уявну частину дії у даній критичній точці \ (\ rho _i \). Це,
Для конкретних дій, які ми розглядаємо, вони набувають таких форм
- Маскування гіркого смаку від Molecules SpringerLink
- Підвищення ефективності екранів за допомогою лінійного електромагнітного двигуна SpringerLink
- Локсапін для скасування антипсихотичних метаболічних порушень Огляд діаграми SpringerLink
- Як змінюються татуювання, коли ви худнете - ідеї татуювань, художники та моделі
- Інкубаційна енергетика Laysan Albatross SpringerLink