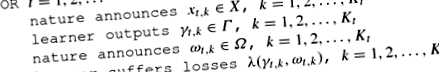Алгоритм агрегування для прогнозування пакетів
Анотація
У цій роботі сформульовано протокол прогнозування пакетів, що є приватним випадком онлайн-прогнозування із затримкою зворотного зв'язку. Згідно з протоколом прогнозування пакетів, той, хто навчається, повинен зробити кілька прогнозів, не бачачи відповідних результатів, і тоді результати виявляються за один раз. Стаття розробляє теорію прогнозування з порадами експертів щодо зграй шляхом узагальнення поняття змішуваності. Ми пропонуємо ряд алгоритмів злиття для прогнозування пакетів з жорсткими найгіршими випадками втрат, подібних до тих, що використовуються для агреговального алгоритму Вовка. На відміну від існуючих алгоритмів налаштувань зворотного зв'язку із зволіканням, наші алгоритми не залежать від порядку результатів у наборі. Емпіричні експерименти на наборах даних про спорт та ціни на будинки проводяться для вивчення ефективності нових алгоритмів та порівняння їх із існуючим методом.
Вступ
Ця стаття стосується он-лайн протоколу прогнозування, де учень повинен передбачити результати \ (\ omega _1, \ omega _2 \ ldots \), що відбуваються послідовно. Учень отримує зворотний зв'язок по ходу.
У базовому он-лайн протоколі прогнозування, на кроці т навчається видає прогноз \ (\ gamma _t \), а потім відразу бачить справжній результат \ (\ omega _t \), який є зворотним зв'язком. Якість прогнозування оцінюється функцією втрат \ (\ лямбда (\ гамма, \ омега) \), вимірюючи невідповідність між прогнозом і результатом або, загалом кажучи, кількісно визначаючи (несприятливий) ефект при прогнозуванні \ (\ гамма \) конфронтує результат \ (\ omega \). Результативність учня оцінюється сукупною втратою Т випробування \ (\ sum _ ^ T \ лямбда (\ gamma _t, \ omega _t) \) .
У цій роботі ми стурбовані проблемою прогнозування за порадами фахівців. Припустимо, що учень має доступ до прогнозів ряду експертів. Перш ніж учень зробить прогноз, він може побачити прогнози експертів, і його мета - зазнати втрат, близьких до втрат найкращого ретроспективно.
У протоколі із затримкою зворотного зв'язку може бути затримка з отриманням справжніх результатів \ (\ omega _t \). Можливо, учню доведеться зробити кілька прогнозів, перш ніж фактично побачити результати минулих випробувань. Ми розглянемо особливий випадок цього протоколу, коли з’являться результати пачки: учень повинен зробити кілька прогнозів, ніж виявляються всі результати, і знову потрібно зробити кілька прогнозів.
Проблема, яка природно вкладається в ці рамки, полягає в сукупності прогнозів букмекерів. Вовк та Жданов (2009) прогнозують результати спортивних матчів на основі ймовірностей, розрахованих на основі шансів, наведених букмекерами. Якщо збіги відбуваються один за одним, проблема, природно, відповідає базовому прогнозуванню за допомогою рекомендацій експертів. Однак загальноприйнято (наприклад, в англійській Прем'єр-лізі), що кілька матчів відбуваються в той же день. Було б природно спробувати спрогнозувати всі результати заздалегідь. Усі матчі того самого дня можна розглядати як зграю в наших рамках.
Ми розробляємо теорію прогнозування з експертними порадами щодо пакетів, розширюючи алгоритм агрегування (AA), представлений Вовком (1990, 1998). У розд. 2.2 та Додаток А, ми досліджуємо існуючу теорію АА для прогнозування одиничних результатів (за нашою термінологією, пакети розміром один). Теорія базується на концепції змішуваність середовищ прогнозування, які називаються іграми. У розд. 3, ми розробляємо теорію змішуваності для ігор з пакетами результатів. Теорема 1 показує, що гра з участю пачок К Результати мають той самий профіль констант змішуваності, що і оригінальна гра з одиночними результатами, але швидкість навчання ділиться на К. Це спостереження дозволяє нам обробляти пачки постійного розміру. Однак, як обговорювалося вище, у справді цікавих випадках розмір упаковки змінюється з часом, і, таким чином, змішуваність середовища змінюється від кроку до кроку. До цієї проблеми можна підходити по-різному, що призводить до різних алгоритмів з різними межами продуктивності. У розд. 4, ми вводимо три Алгоритми агрегування для прогнозування пакетів, AAP-max, AAP-інкрементальний та AAP-струм і отримують найгірші верхні межі їх сукупних втрат.
Загальна теорія АА (Вовк, 1998) дозволяє нам показати у розділі. 5, що в якомусь сенсі наші межі є оптимальними. У розд. 5.1, ми пропонуємо автономне виведення нижньої межі для системи змішаних втрат Адамського та ін. (2016). Однак питання оптимальності упаковки ще далеко не повністю вирішене і вимагає подальшого дослідження.
Як вже згадувалося раніше, проблему прогнозування пакетів можна розглядати як окремий випадок проблеми із зволіканням із зворотним зв’язком. Ця проблема вивчалась здебільшого в рамках он-лайн опуклої оптимізації (Zinkevich 2003; Joulani et al. 2013; Quanrud and Khashabi 2015). Термінологія та підхід до он-лайн опуклої оптимізації відрізняється від нашої, яка сягає Літлстоуна та Уормута (1994) та була обстежена Цеза-Б'янкі та Лугосі (2006).
Проблему прогнозування за допомогою поради фахівців щодо зволікання із зворотним зв’язком можна вирішити, запустивши паралельні копії алгоритмів, що передбачають одиничні результати. У розд. 2.3, ми описуємо алгоритм Паралельні копії, який, по суті, СМІЛИЙ від Joulani et al. (2013) з використанням алгоритму агрегування як базового алгоритму для окремих результатів. Теорія агреговуючого алгоритму передбачає найгірший верхній випадок втрати паралельних копій. Ми бачимо, що термін жаління множиться на максимальну затримку або розмір упаковки, як у існуючій літературі (Joulani et al. 2013; Weinberger and Ordentlich 2002).
Межі, які ми отримуємо для наших нових алгоритмів, однакові (AAP-max та AAP-інкрементальні) або несумісні (AAP-струм) з обмеженнями для паралельних копій. Ми обговорюємо межі в секті. 5, а потім у розд. 6 проводять емпіричне порівняння продуктивності алгоритмів.
Для експериментів ми прогнозуємо результати спортивних матчів на основі шансів букмекерів і визначаємо ціни на будинки на основі описів будинків. Спортивні набори даних включають футбольні матчі, які, природно, містять пакети, та тенісні матчі, де ми представляємо пакети штучно двома різними способами. Набори даних про ціни на житло містять записи про майнові операції в Еймісі в США та районі Лондона. Набори даних фіксують лише місяць транзакції, тому вони природно організовані в пакети. Експерименти з цінами на житло дотримуються підходу Kalnishkan et al. (2015): передбачення за порадами експертів можна використовувати для пошуку відповідної минулої інформації. Передбачувачі, навчені різним розділам минулих даних, можна комбінувати в режимі он-лайн, щоб відповідні минулі дані використовувались для прогнозування.
Ефективність алгоритму паралельних копій залежить від порядку результатів у пакетах, тоді як наші алгоритми не залежать від порядку. Ми порівнюємо сукупну втрату наших алгоритмів із втратою паралельних копій, усередненою за випадковими перестановками в пакетах. Ми прийшли до висновку, що хоча паралельні копії можуть працювати дуже добре, особливо якщо порядок результатів у пакетах містить корисну інформацію, втрата наших алгоритмів завжди близька до середньої втрати паралельних копій, а деякі алгоритми перевершують середнє.
Потім ми порівнюємо наші алгоритми між собою, роблячи висновок, що AAP-max є найгіршим, і AAP-струм перевершує AAP-інкремент, якщо відношення максимуму до мінімального розміру упаковки невелике.
Попередні етапи та передумови
У цьому розділі ми представляємо основу прогнозування пакетів та оглядаємо зв’язки з літературою.
Протоколи для прогнозування пакетів
Гра \ (\ mathfrak = \ langle \ varOmega, \ varGamma, \ lambda \ rangle \) є трійкою результат простір \ (\ varOmega \), простір прогнозування \ (\ varGamma \) та функція втрат \ (\ лямбда: \ varGamma \ times \ varOmega \ rightarrow [0, + \, \ infty] \) .
Результати \ (\ omega _1, \ omega _2, \ ldots \ in \ varOmega \) відбуваються послідовно. A учень або стратегія прогнозування виводить прогнози \ (\ gamma _1, \ gamma _2, \ ldots \ in \ varGamma \) перед тим, як бачити відповідні результати. Учень може мати доступ до якоїсь побічної інформації; ми скажемо, що той, хто навчається, бачить сигнали \ (x_t \), що надходить з сигнальний простірX.
У класичному протоколі учень робить прогноз (можливо, за допомогою сигналу), а потім результат негайно розкривається. У цій роботі ми розглядаємо розширення цього протоколу та дозволяємо отримати результати пачки можливо різного розміру. Той, хто навчається, повинен створити пакет прогнозів, перш ніж побачити справжні результати. Наступний протокол узагальнює структуру.
Протокол 1
(Прогнозування пакетів)
На кожному суді т учень повинен робити прогнози \ (K_t \), а не один. Ми будемо говорити про пакет прогнозів учня \ (\ gamma _ \ in \ varGamma \), \ (k = 1,2, \ ldots, K_t \), пакет результатів \ (\ omega _ \ in \ varOmega \), \ (k = 1,2, \ ldots, K_t \) тощо.
У цій роботі ми припускаємо повне інформаційне середовище. Учень знає \ (\ varOmega \), \ (\ varGamma \) та \ (\ lambda \). Він бачить усіх \ (\ omega _ \), коли вони стають доступними. З іншого боку, ми не робимо припущень щодо механізму, що генерує \ (\ omega _ \), і будемо зацікавлені в найгірших гарантіях збитків. Результати не повинні задовольняти ймовірнісним припущенням, таким як i.i.d., і можуть поводитися зловмисно.
Тепер нехай \ (\ mathcal_1, \ mathcal_2, \ ldots, \ mathcal_N \) будуть учнями, що працюють згідно з Протоколом 1. Ми будемо називати цих учнів як експерти. Припустимо, що на кожному ході їх прогнози стають доступними для учня \ (\ mathcal \) як особливий вид побічної інформації. Потім учень працює згідно з наступним протоколом.
Протокол 2
(Прогнозування пакетів з порадами фахівців)
Мета учня в цій установці - зазнати втрат, близьких до найкращого експерта в ретроспективі (в будь-якому формальному сенсі, якого можна досягти). Ми шукаємо стратегії злиття для того, хто навчається, переконуючись, що той, хто навчається, досягає низьких кумулятивних втрат порівняно з експертами; ми побачимо, що кількісну оцінку кумулятивних втрат можна по-різному.
Стратегії злиття, які нас цікавлять, можна обчислити в якомусь природному сенсі; ми не будемо робити точних тверджень про обчислюваність. Ми не накладаємо жодних обмежень на експертів. Далі читач може замінити пункт «для всіх прогнозів \ (\ gamma _ (i) \), що з’являється в Протоколі 2», більш інтуїтивним реченням «для всіх експертів».
Цей протокол може мати незначні варіації. Замість того, щоб отримувати всі прогнози \ (K_t \) від кожного експерта одночасно, учень може отримувати прогнози для кожного результату по одному і робити свої власні, перш ніж бачити наступний набір прогнозів експертів. Для більшості нашого аналізу це не має значення, як ми побачимо пізніше. Можливо, учню доведеться працювати над кожною «зграєю» прогнозів експертів послідовно, навіть не знаючи її розмір заздалегідь. Важливо лише те, що результати приходять за один раз після того, як учень закінчить прогнозування зграї.
Пакети одного розміру
Для пакетів розміром 1 (\ (K_t = 1 \), \ (t = 1,2, \ ldots \)), Агрегуючий алгоритм (AA) від Vovk (1990, 1998) вирішує проблему прогнозування за допомогою експертних рекомендацій у дуже загальний сенс.
Алгоритм базується на понятті змішуваність.
Розгляньте гру \ (\ mathfrak = \ langle \ varOmega, \ varGamma, \ lambda \ rangle \). Константа \ (C> 0 \) є допустимий для швидкість навчання \ (\ eta> 0 \), якщо для кожного \ (N = 1,2, \ ldots \), кожного набору передбачень \ (\ gamma (1), \ gamma (2), \ ldots, \ gamma (N) \) та кожен розподіл \ (p (1), p (2), \ ldots, p (N) \) (такий, що \ (p (i) \ ge 0 \) та \ (\ sum _ ^ Np ( i) = 1 \)) існує \ (\ gamma \ in \ varGamma \), що забезпечує для всіх результатів \ (\ omega \ in \ varOmega \) нерівність
константа змішуваності \ (C_ \ eta \) - мінімум усіх \ (C> 0 \), допустимих для \ (\ eta \). Зазвичай цей мінімум досягається. Наприклад, це досягається для всіх \ (\ eta> 0 \), коли \ (\ varGamma \) є компактним, а \ (e ^ \) - безперервна виноска 1 у \ (\ gamma \) .
Алгоритм агрегування приймає швидкість навчання \ (\ eta> 0 \), константу C. допустимо для \ (\ mathfrak \) з \ (\ eta \) та попереднього розподілу \ (p (1), p (2), \ ldots, p (N) \) (\ (p (i) \ ge 0 \) та \ (\ sum _ ^ Np (i) = 1 \)) для експертів \ (\ mathcal_1, \ mathcal_2, \ ldots, \ mathcal_N \) .
Ми використовуємо позначення
для сукупної втрати учня та експертів (оскільки розмір пакета завжди дорівнює 1, ми опускаємо другий показник k і напишіть, скажімо, \ (\ omega _t \) замість \ (\ omega _ \)). Наступна пропозиція надає верхню межу втрати учня.
Пропозиція 1
(Вовк 1990, 1998) Нехай C. бути допустимим для \ (\ eta> 0 \). Тоді для кожного \ (N = 1,2, \ ldots \), втрата учня \ (\ mathcal \) з використанням AA з \ (\ eta \) та попереднім розподілом \ (p (1), p ( 2), \ ldots, p (N) \) задовольняє
для кожного експерта \ (\ mathcal_i \), \ (i = 1,2, \ ldots, N \), усіх часових горизонтів \ (T = 1,2, \ ldots \), і всіх результатів, зроблених природою. \(\Майдан \)
Псевдокод Агрегуючого алгоритму та доказ пропозиції наведені в Додатку А.
Вибір конкретної швидкості навчання залежить від величини констант змішуваності. Для деяких ігор ми маємо природний оптимальний вибір. Наприклад, розглянемо загальну гру на квадратні втрати з використанням \ (\ varOmega = \ varGamma = [A, B] \) та \ (\ lambda (\ gamma, \ omega) = (\ gamma - \ omega) ^ 2 \) для експериментів у цій роботі. Це одна з так званих змішується ігри с C. досягнення 1. Природний вибір \ (\ eta \) тоді є таким максимальним значенням, що \ (C_ \ eta = 1 \); це мінімізує другий доданок у правій частині (2). Таке \ (\ eta \) задано \ (\ eta _0 = 2/(B-A) ^ 2 \); можна легко адаптуватися до інтервалу [A, B] виведення Вовка (2001) для інтервалу \ ([- \, Y, Y] \) .
Примітка 1
Для загальної гри з квадратними втратами, якщо використовується швидкість навчання \ (\ eta _0 \), можна знайти значення \ (\ gamma \), що задовольняє (1) для всіх \ (\ omega \ в [A, B] \) з використанням явного функція заміщення
слідом за Вовком (2001). Це робить алгоритм агрегування для загальної гри з квадратними втратами ефективним.
Для ігор, що не змішуються (таких як гра на абсолютну програшу з \ (\ лямбда (\ gamma, \ omega) = | \ gamma - \ omega | \)), bound (2) забезпечує компроміс. Оптимізація обмежень є більш складним завданням і може вимагати припущень щодо поведінки експертів або часового горизонту Т.
Важливість АА випливає з результатів Vovk (1998). За деяких м’яких припущень щодо регулярності гри та при рівномірному початковому розподілі можна показати, що константи в нерівності (2) є оптимальними. Якщо будь-яка стратегія злиття досягає гарантії (з \ (A> 0 \))
для всіх експертів \ (\ mathcal_1, \ mathcal_2, \ ldots, \ mathcal_N \), \ (N = 1,2, \ ldots \), усі часові обрії Т, і всі результати, тоді AA з рівномірним попереднім розподілом \ (p (i) = 1/N \) і деяким \ (\ eta> 0 \) забезпечує гарантію з однаковим або нижчим C. і A. Ми детальніше обговоримо цей результат у Додатку А.
Підхід зволікання із зволіканням
Протокол прогнозування з пакетами, який ми описуємо, можна розглядати як окремий випадок параметрів зволікання із зворотним зв’язком, оглянутих Джоулані та співавт. (2013).
У прогнозованому зворотному зворотному зв’язку з протоколом консультацій експертів на кожному кроці учень отримує лише один раунд прогнозів від кожного експерта і повинен виробляти свої власні. Однак результат, що відповідає цим прогнозам, може стати доступним пізніше. Якщо це буде розкрито на тому самому судовому процесі, що і в Розділі. 2.2, ми говоримо, що затримка одна. Якщо це буде виявлено під час наступного випробування, затримка дорівнює двом і т. Д. Передбачення кількості упаковок, що не перевищує К може розглядатися як передбачення із затримками, що не перевищують К.
Алгоритм BOLD (Joulani et al. 2013) для цього протоколу працює наступним чином. Візьміть алгоритм, що працює із затримками 1 (або пакетами розміром 1); ми будемо називати його базовим алгоритмом. Для об’єднання прогнозів експертів ми запустимо кілька копій базового алгоритму. Вони незалежні в тому сенсі, що не діляться інформацією. Кожна копія неодноразово отримуватиме прогнози експертів щодо об’єднання, видаватиме прогноз, а потім чекатиме результату, відповідного прогнозу. Кожний момент копія базового алгоритму або знає всі результати передбачень, які він зробив, або очікує результату, відповідного останньому прогнозу. У першому випадку ми говоримо, що копія готова (для об’єднання більшої кількості прогнозів експертів), а в наступному випадку ми говоримо, що копія заблокована (і не може об’єднуватися).
На кожному випробуванні, коли надходить новий раунд прогнозів експертів, ми вибираємо готовий алгоритм (скажімо, такий, що має найменшу кількість) і надаємо йому прогнози експертів. Він виробляє прогноз, який ми передаємо далі, і алгоритм блокується, поки не з’явиться результат цього випробування. Якщо в даний час всі алгоритми заблоковані, ми запускаємо нову копію базового алгоритму.
Припустимо, що ми граємо в гру \ (\ mathfrak \) та C. допустимо для \ (\ mathfrak \) зі швидкістю навчання \ (\ eta \). Для базового алгоритму візьмемо АА с C., \ (\ eta \) та початкові ваги \ (p (1), p (2), \ ldots, p (N) \). Якщо затримка ніколи не перевищує D, нам ніколи не потрібно більше ніж D алгоритми в масиві, і кожен з них зазнає втрат, що задовольняють пропозицію 1. Підсумовуючи межі, отримуємо, що втрата \ (\ mathcal \) за допомогою цієї стратегії задовольняє
для кожного експерта \ (\ mathcal_i \), де сума в \ (>> _ T \) береться за всі результати, виявлені до кроку \ (T + 1 \). Значення D не потрібно знати заздалегідь; ми завжди можемо розширити масив із збільшенням затримки. Ми будемо називати комбінацію BOLD і AA вищезазначеним способом як Паралельні копії алгоритм.
Для Протоколу 2 ми можемо визначити прості кумулятивні втрати
- 10 найкращих домашніх наборів для обличчя з лимоном для чистої шкіри
- 10 упаковок маски для схуднення V-подібної форми
- Зовнішній вигляд проти здоров’я Чи впливає причина дієти на дієтичну поведінку SpringerLink
- 2019 Нова дорожня прихована сумка з грошима для грошей Кумедний пакет Протиугінні поясні пакети Сумка-гаманець Fanny Bag
- 5 домашніх наборів для обличчя з корицею